
编码的奥秘_7十进制计数法 |
|
语言仅仅是一种编码的想法似乎很容易被人们接受,很多人在学生时代至少学过一种外语,因此,我们知道在英语中“cat”(猫)也可以被叫作gato、chat、Katze、KOIIIK或kapa。 然而,数字不那么容易随文化的不同而改变。不论那种语言,也不管怎样读那些数字,地球上我们能够遇到的几乎所有的人都用同样的方式来写数字: 👨🎨🧢🔌☠🤛 0 1 2 3 4 5 6 7 8 9 数学,从某种意义上来说是不是可以称得上是一种世界语言呢?毫无疑问,数字是我们平时能够接触到的最抽象的代码。当你看到数字“3”时并不需要立即将它和任何事情相联系。你可能将它设想为3个苹果或者3个其他什么东西,但是当你从上下文中得知这个数字是指某个小孩的生日、电视频道、曲棍球比赛的得分或者是制作蛋糕的食谱中提供的需要面粉的杯数时,也能够像认为它代表3个苹果时一样自然。 因为数字一开始产生时就很抽象,所以让我们理解这些苹果: 👦👠📮😴🧠 
并不一定要用符号“3”来表示就更困难了。本章的很大一部分以及下一章将来讲解这些苹果: 也可以用“11”的形式来表示。 🙌🚘🧊❌🐋 先不讨论数字10与生俱来的特殊性。大多数人使用的数字系统是基于10(有时候是5)的,这种情况并不奇怪。最初人们是用手指来数数的。要是人类进化成有8个或12个手指,人类计数的方式就会有所不同。英语Digit(数字)这个单词也可以指手指或脚趾,单词five(五)和单词fist(拳头)有相同的词根,这种情况并不是巧合。 这样看来,人类选择使用以10为基础的记数方法(或称为十进制记数法)完全是任意的,但我们赋予10的整数次幂重大的意义,并给它们命名:十个一年是一个十年;十个十年是一个世纪;十个世纪是一个千年;千个一千是百万;千个百万是十亿。下面是10的各次幂: 🖕🗺🥩🅰🦚 10^1=10 10^2=100 10^3=1000(千) 10^4=10000 👃🔥🍚💲🦖10^5=100000 10^6=1000000(百万) 10^7=10000000 10^8=100000000 10^9=1000000000(十亿) 👨⚕️🥾🛋😇👃 多数历史学家认为数字最初创造出来是用来数东西的,比如:人数、财产数、商品交易量等。举个例子来说,假定某个人有4只鸭子,他可能画4只鸭子作为记录: 
后来,专门负责画鸭子这项工作的人想:“我为什么一定要画4只鸭子呢?为什么不能只画1只鸭子,然后用其他方法(管它用什么方法,哪怕用一条竖线来代表一只鸭子)来表示有4只呢?” 
🤞🚘🌰🆗 但若某人有27只鸭子,用画竖线来表示鸭子只数的方法就显得很荒谬了: 
于是,有人想到得有一种好的办法才行,数字系统就这样诞生了。 👂🌞🥭™🦋 在早期的数字系统中,只有罗马数字系统沿用至今。钟表的表盘上常常使用罗马数字,此外它还用来在纪念碑或雕像上标注日期、标注书的页码,或作为提纲条目的标记。最令人惊奇的是罗马数字常用在电影中做版本说明。(只要你有足够快的速度将字幕结尾处出现的MCMLIII译码,通常情况下就可以回答“这部影片是什么时候拍的”这个问题。) 27只鸭子可以用罗马数字这样表示: 👁🚗🌶❓🪶 
这里用到的概念非常简单:X代表10条竖线,V代表5条竖线。 现在仍在使用的罗马数字有: 🙌🚤🥣🕊 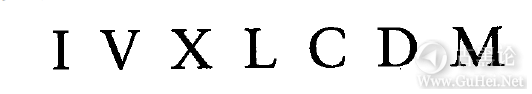
字母I代表一个一,这可能来自于一条竖线或者伸出的一个手指。字母V很可能是一只手的符号,代表五;两个字母V组成字母X,代表十;字母L代表五十;字母C来自于拉丁文中表示一百的单词—centum;字母D代表五百;最后,字母M来自拉丁文中的单词—mille,代表一千。 也许你不一定同意,很长一段时间以来,罗马数字被认为用来做加减运算非常容易,这也是罗马数字能够在欧洲被长期用于记帐的原因。事实上,当对两个罗马数字进行相加运算时,只需将这两个罗马数字的所有符号合并然后用下面的方法将其简化:五个I是一个V,两个V是一个X,五个X是一个L,等等。 🤞🌧‼🐡 但使用罗马数字做乘除法是很难的。很多其他早期的数字系统(比如古希腊数字系统)和罗马数字系统相似,它们在做复杂运算时存在一定的不足。尽管如此,古希腊人所发明的非凡的几何学至今仍是中学的一门课程,古希腊人不是以代数享誉世界的。我们现在使用的数字系统通常称为阿拉伯数字系统,或称为印度—阿拉伯数字系统。它起源于印度,但由阿拉伯数学家传入欧洲。一位著名的波斯数学家—Muhammed ibn-Musaal-Khwarizmi(由它的名字得到单词algorithm(算法))在大约公元825年写了一本代数书,书中用的就是印度的数字系统(阿拉伯数字)来计数。产生于公元1120年的拉丁文译本对整个欧洲用现在的阿拉伯数字代替当时使用的罗马数字的过渡过程产生了很大的影响。 🧒👖📡🤖👁 印度—阿拉伯数字系统与先前的数字系统相比在以下三个方面不同: 印度-阿拉伯数字系统是和位置相关的,也就是说,一个数字依据位置的不同代表不同的数量。数字的位置和数字的大小一样,都是很重要的。(但实际上,数字的位置更重要。)100和1000000中都只有一个1,但我们知道一百万比一百要大得多。 几乎所有早期的数字系统都有一个阿拉伯数字所没有的东西,那就是用来表示数字10的一个专门的符号。现在使用的数字系统中是没有代表10的专门符号的。 👨🎨🎩🔍😔👂 另一方面,几乎所有早期的数字系统都缺少一个阿拉伯数字中有的,而且事实证明是比代表数字10的符号重要得多的符号,那就是零。 是的,就是零。这个小小的零毫无疑问是数字和数学历史上最重要的发明之一。它支持位置表示法,因为它可以将205与250区别开来。数字零也使得与位置无关的数字系统中非常复杂的运算变得简单,尤其是乘除法。 ✊⛄♀🦌 印度——阿拉伯数字的整体结构是以读它们的方式展现的。拿4825作为例子,我们把它读 作“四千八百二拾五”,意思是: 四个一千 八个一百 两个十 一个五 👆🚈🍏💲🪶 或者,可以将它的组成写成这样: 4825=4000+800+20+5 或者,可以将它进一步分解,写成这样: 👨🎨💄📬🥰🖕 4825=4×1000+ 8×100+ 2×10+ 5×1 另外,也可以使用10的整数次幂的形式,重新写成: 4825=4×10^3+ 8×10^2+ 2×10^1+ 5×10^0 记住,任何数的0次幂都等于1。  🤙🦼🥩❌🦉 多位数中的每位都有特定的意义,如下图所示。这7个方格可以表示从0~99999999的任何一个数字: 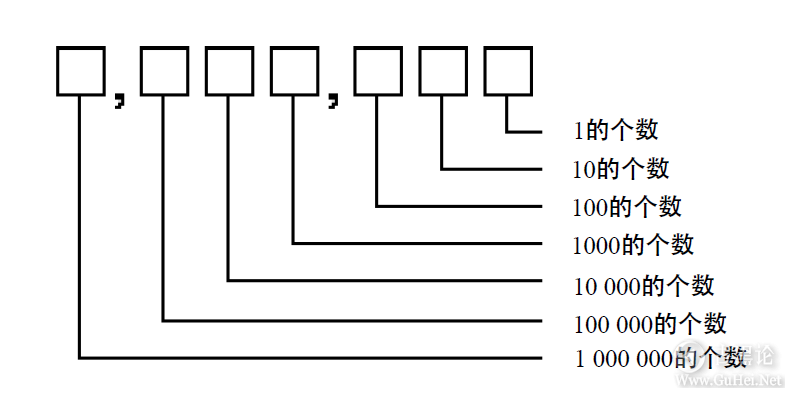
每一个位置(位)与10的一个整数次幂相对应。不需要一个专门的符号来表示数字10,因为可以将1放在不同的位置,用0作为占位符。 ✌🪐🫖🆗🦬 分(小)数可以同样的形式作为数字放在十进制数的小数点的右边,这一点非常好。数字42705.684是: 4×10000+ 2×1000+ 7×100+ 0×10+ 5×1+ 6÷10+ 8÷100+ 4÷1000 👳🗝😘🤳该数也可以写成不带除法的形式,如下: 4×10000+ 2×1000+ 7×100+ 0×10+ 5×1+ 6×0.1+ 8×0.01+ 4×0.001 或写成10的整数次幂的形式: 👦🧢📮😴🤞 4×10^4+ 2×10^3+ 7×10^2+ 0×10^1+ 5×10^0+ 6×10^-1+ 8×10^-2+ 4×10^-3 注意10的指数是怎样变到零再变成负数的。 我们知道,3加上4等于7。同样,30加上40等于70,300加上400等于700,3000加上4000等于7000。这正是阿拉伯数字系统的“魅力”所在,无论你进行多长的十进制的加法,只要根据一种方法将问题分成几步即可。 🧑🚀👞😃🧠 每一步最多只是将两个一位数字相加,这也是很久以前有人强迫你记加法表的原因: 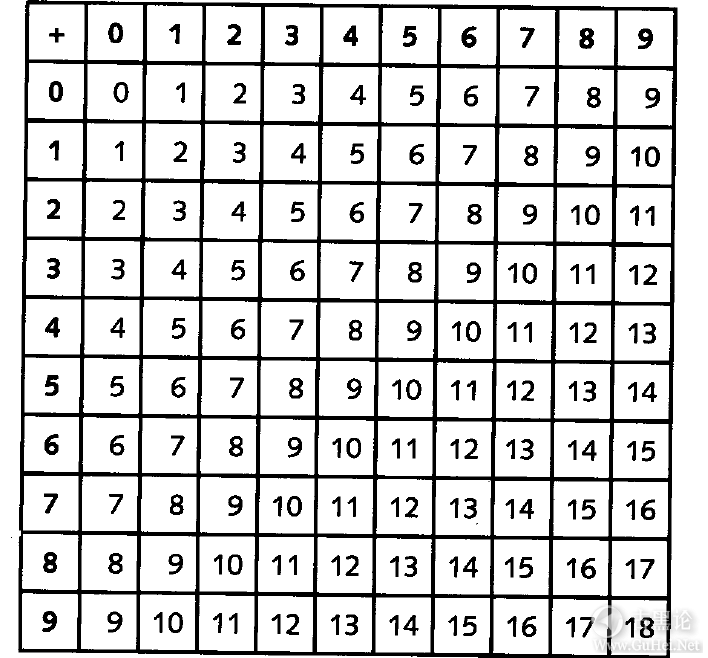
🙌🎢🥣™🐺 从最上边的一行和最左边的一列找到要相加的两个数字,在行与列的交叉点上找到它们相加的结果。例如,4加上6等于10。 同样,做两个十进制数相乘的运算时,方法可能稍稍复杂一点儿,但仍然只需将问题分成几步,这样就不会比做加法和一位数的乘法更复杂了。你在小学时可能也必须记住下面的乘法表: 👌🚤🍞🈚🦟 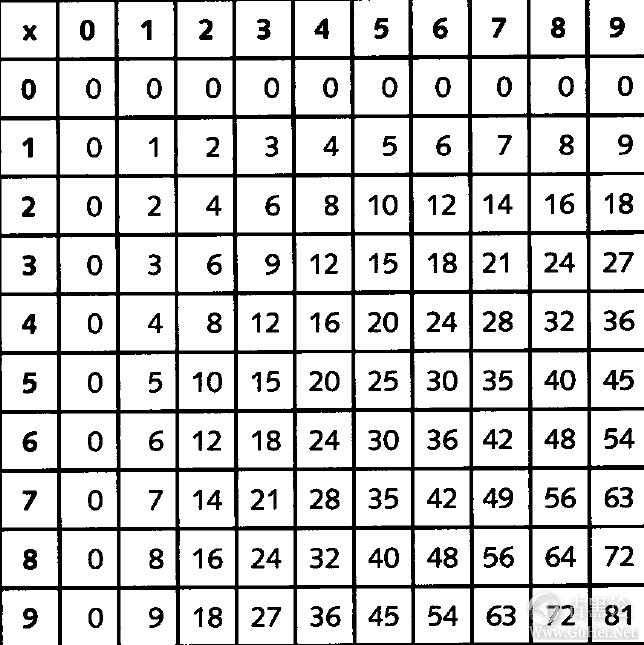
与位置相关的记数系统的优点不在于它多么好用,而在于当它用在不是十进制的系统中时,也一样的好用。我们现在用的数字系统不一定适合所有的人。十进制数字系统的一个很大问题就在于它和卡通人物没有任何关系。大多数的卡通人物每只手上只有4个手指,因此它们喜欢基于8的数字系统(八进制)。 🤞🗽🦀🈸🦠 有趣的是,我们所知的大部分关于十进制数的知识同样可以用于卡通朋友所喜爱的八进制数字系统中。
帖子热度 1万 ℃
|
|
|
|
|

 变色卡
变色卡 古黑论管理员,在论坛上有什么问题都可以找他。
古黑论管理员,在论坛上有什么问题都可以找他。