
编码的奥秘2_编码与组合 |
|
摩尔斯电码由萨缪尔·摩尔斯(1791·1872)发明。摩尔斯电码是随着电报机的发明而产生的,电报机我们以后也还要做详尽的说明。正如摩尔斯电码很好地说明了编码的本质一样,电报机也提供了理解计算机硬件的良好途径。
大多数人认为摩尔斯电码的发送易于接收,即使你没有记住摩尔斯电码,也可以方便地借助下面这张按字母顺序排列的表发送: 👨🎨🦺🛋😷👄 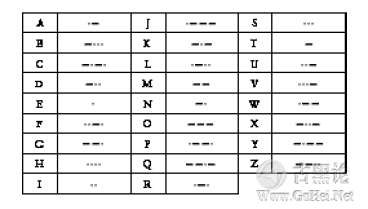
接收摩尔斯电码并将其翻译回单词比发送费时费力多了,因为译码者必须反向地将已编码的"滴-嗒"序列与字母对应。例如,在确定接收到的字母是“Y"之前,必须按字母逐个地对照编码表。 问题是我们仅有_张提供"字母—摩尔斯电码"的编码表,而没有一张可供逆向查找的"摩尔斯电码—字母"译码表。在学习摩尔斯电码的初级阶段,这张译码表肯定会提供很大的便利。然而,如何构造译码表却毫无头绪,因为我们似乎无法找出这些按字母顺序排列的"滴-嗒"序列的规律。 🖕🎢🥑🈸🐂 那么忘记那些字母序列吧,也许按照码字中"滴""嗒"的个数来排列会是个更好的尝试。例如,仅含一个"滴"或"嗒"的摩尔斯电码序列只可能代表E或T这两个字母之 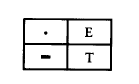
🙏⛵🍒📳🐺 两个"滴"或"嗒"的组合则代表了4个字母I、A、N、M: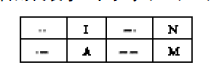
三个"滴"或"嗒"的序列代表了8个字母: 👊🦼🍌❗🐝 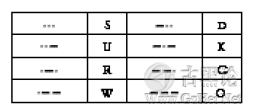
最后(如果不考虑数字和标点符号的摩尔斯电码),四个"滴"或"嗒"的序列则共代表了16个字母: 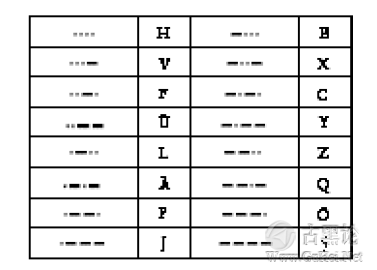
👀🏠🌰🆗 在翻译别人发送的摩尔斯电码时,上面4张表提供了极大的便利。当你接收到_个代表特定字母的码字时,按其中含有的"滴""嗒"个数,至少可以跳到其对应的那张表中去查找。每张表中,全"滴"的字母排在左上角,全"嗒"的字母排在右下角。 你注意到4张表大小的规律了吗?每张表都怡好是其前一张表的两倍大小。这其中包含的意义是:前一张表的码字后加一个"滴"或加一个"嗒“,即构成了后一张表。 🙌⛄🫑↔🐴 可以按下面的方式总结这个有趣的规律: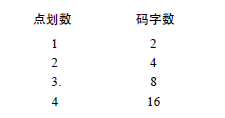
四张表中每张码字数都是前_张的两倍,那么如果第一张表含2个码字,第二张表则含2X2个码字,第三张表2X2X2个码字。以下是另一种表达方式: 🤛🚐🍌🅿🦊 
当然,如果遇到数的自乘,可以用幂表示,例如2X2X2X2可以写成24。数字2、4、8、16分别是2的1、2、3、4次幂,因为可以用依次乘2的方法将它们计算出来。由此我们的总结还可以写成下面的方式: 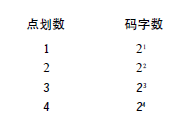
这张表简单明了,码字数是2的次方,次方数目与码字中含有的"滴""嗒"数目相同。我们可以把表总结为一个简单的公式: 🦴🪐🥚🚷🪶 码字数=2“滴"与“嗒"的数目 很多编码中都用到2的幂,在下一章中我们会看到另一个例子。为了使译码的过程更为简便,可以画出如下一张树形图: 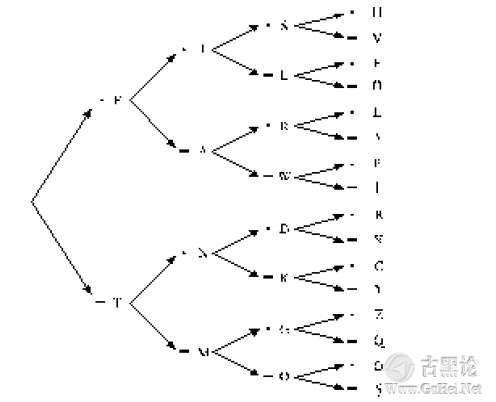
👃🪐🧊🈸🦠 这张表表示出了由"滴"与"嗒"的连续序列得出的字母。译码时,按箭头所指从左到右进行。例如,你想知道电码"滴-嗒-滴"代表的字母,那么从最左边开始选择点,沿箭头向右选择划,接着又是点,得出对应的字母是R,它写在最后一个点的旁边。 如果认真考虑,会发现事先建立这样一张表是定义摩尔斯电码所必需的。首先,它保证了你不会犯给不同的字母相同码字的错误丨其次,它保证你使用了全部的可用码字,而没有使"滴"与"嗒"的序列毫无必要的冗长。 我们可以加长码字至5位或更长,5位长的码字又提供了额外的32(2X2X2X2X2或25)个码字。一般而言,这就足够10个数字和16个标点符号使用。实际上,摩尔斯电码中的数字确实是5位的,但在许多其他编码方式中,5位码字常用于重音字母而不是标点符号。🦺📠🤬🖐 为了包含所有的标点符号,系统必须扩充至6位表示,提供64个附加编码,此时系统可表示2+4+8+16+32+64共126个字符。这对摩尔斯电码而言太多了,以至于留下许多"未定义〃的码字。此处"未定义"指不代表任何意义的码字,如果在你接收的摩尔斯电码中有未定义的码字,就可以肯定发送方出了差错。 由于推出了下面这条公式: 🖕🗼🍼🆎🐞 码字数=2“滴"与"嗒"的数目 我们就可以继续导出更长的码字位数所代表的码字数目。很幸运,我们不必为确定码字数目而写出所有可能的码字,我们所要做的不过是不断地乘2而已: 点划数 码字数 
👏🚘🍇®🦠 摩尔斯电码被称为二元码(binary code),因为编码中仅含"滴"和"嗒"。这与一个硬币很相似,硬币着地时只可能是正面或反面。二元事物(例如硬币)、二元编码(例如摩尔斯电码)常常用2的乘方来描述。 上面所做的对二元编码的分析在数学上的_个分支一组合学或组合分析里只能算是一个简单的练习。传统上,由于组合分析能够用来确定事件出现的几率,例如硬币或骰子组合的数目,所以它常用于概率统计,但它也同样有助于我们理解编码的合成与分解。
帖子热度 8739 ℃
|
|
|
 「古黑浩劫」
「古黑浩劫」
 变色卡
变色卡 古黑论管理员,在论坛上有什么问题都可以找他。
古黑论管理员,在论坛上有什么问题都可以找他。